Using Inquiry Maths To Encourage Students To Build Confidence In Their Mathematical Thinking
- By Alfie Benson
Over the last half term, I have been placed in my Contrasting Placement School which has been an amazing opportunity for me to observe practice in another Maths department and experience a different curriculum model. The school I was placed at follow a well-known pre-made curriculum where the lessons need only to be adapted to fit the group you are teaching. From my observations, I noticed that across many classes in the department the students were largely being delivered a lesson at the front with teacher modelling and then given the worksheet from the pre-made scheme to practice independently while the teacher circulates. I fully understand the need for independent practice and the importance of explicit modelling but when this is largely the main form of delivery I feel it takes away the joy of learning Maths and does not really adopt what the subject is really about. For a mathematician who carries out ‘an everyday job’ (as the students put it), they are not usually just replicating a process they have seen once or twice before but instead questioning, conjecturing, listening to others and of course problem solving. In my experience, the feeling of struggle in solving a problem is a really valuable one for developing a stronger mathematician and one who will want to be curious about solving problems.
As part of my subject development days with our regional expert, we looked at how we can include elements of investigation/inquiry into our lessons to establish a culture of collaboration and curiosity when learning so that students are able to meet new concepts in more meaningful ways and encourages them to take more responsibility for their learning. Clearly, giving students something to investigate and setting them off is not necessarily a good approach. However allowing the students to regulate their own thinking whilst you direct discussions and point them in certain directions with your questioning means students can develop higher order thinking skills that will set them up with the right skills when they inevitably come across problems they find tricky later on in their mathematical career at school or work.
I decided that I would try this investigation style lessons with my Year 8 group who I felt
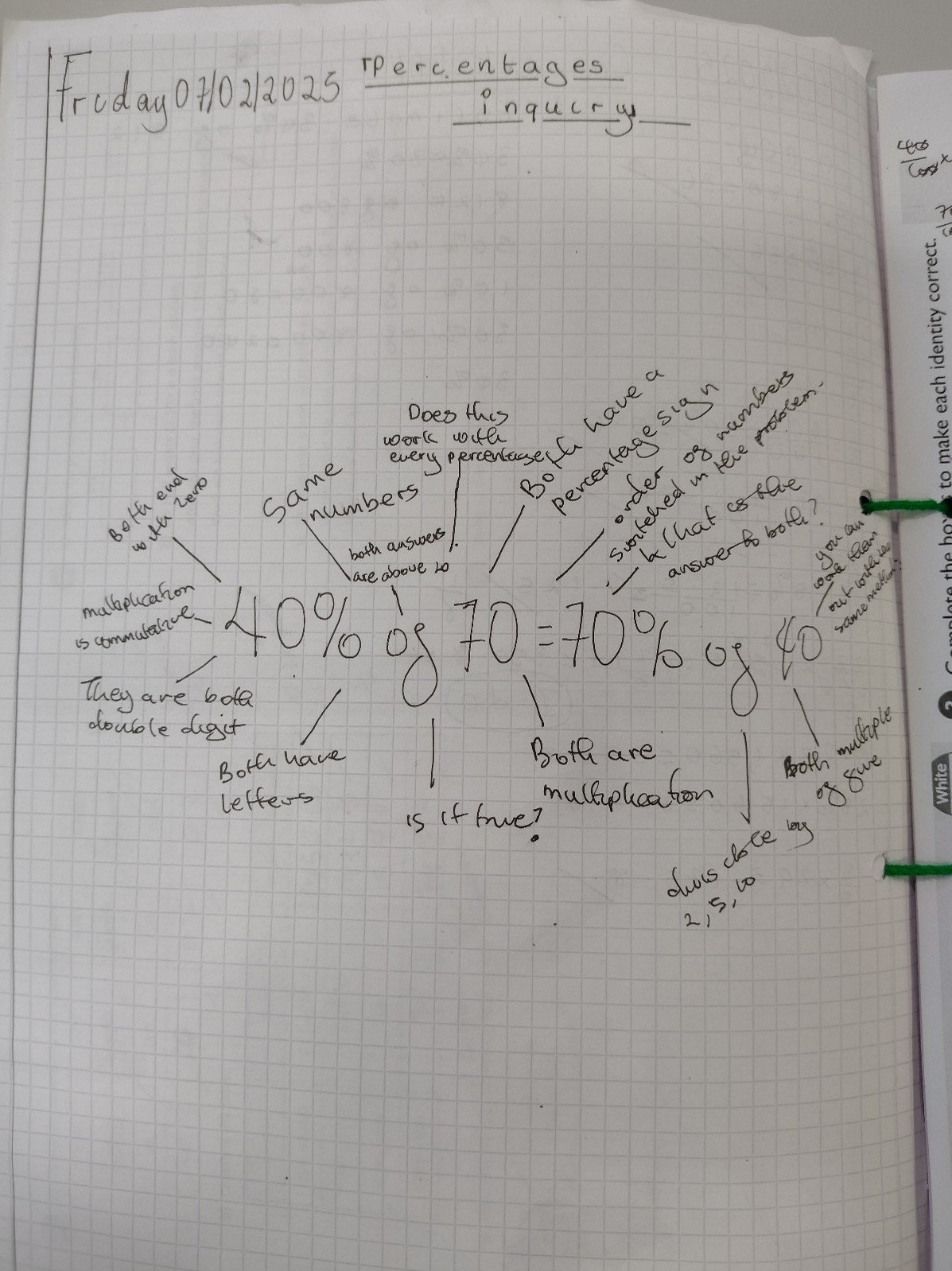could really benefit from developing their mathematical questioning skills. I posed the statement 40% of 70 = 70% of 40 on the board and told my students that I understand they were probably able to quickly work out the answer to both sides of this equation but this was not our aim. They placed a bubble in the middle of their page and I gave them 5 minutes to write down as many observations as they could as well as any questions that they had about the statement. As I circulated, I started to notice some students were simply stating ‘it is true’ or working out the answers so I scaffolded by prompting them with some questions I was thinking such as ‘does this work for all numbers or is it special for just 40 and 70?’, ‘why does this work?’ and ‘can I re-write this in a different way?’. Once I had seen evidence they were starting to get the idea, I gave them 5 minutes to talk to their partner to share what they had and add to their diagram which was really powerful for developing their mathematical oracy. I asked them to discuss in their pairs which statement/question they had which they thought nobody else in the room had. We then came back together as a class and I went round each pair asking for their statement to add to my diagram on the board. This led to some great discussions with the students about why they had chosen their statement/question giving them the opportunity to justify their thinking aloud. When the students began to realise that there was not an incorrect answer when it came to inquiry, they were really invested in asking more questions and making further observations.
We then moved into the explore stage of the inquiry where students take different aspects of the inquiry to investigate in their pairs.
They had statements about 40 and 70 being multiples of 10 and 5 so they decided to try non-multiples of 5 to see if it still works. Others said they were only 2 digits so investigated what
happens with 3 digits. Others investigated what happened with negatives or decimals. After some time, we again came back together and students came up to the other whiteboard to share their examples that proved/disproved their question/statement. We had a rich set of examples and students had tried things out like converting the percentages to decimal multipliers and then multiplying or converting the percentages to fractions – all the skills we had looked at over the week. It also opened up conversations about commutativity that we had earlier in the week leading to one students suggestion that finding percentages is just multiplication so these calculations are commutative which led to echoes of ‘oh yeah!’ from the others.
I asked the students whether they thought that these examples we had was enough to prove this for all numbers – most thought it was good enough, including the other teacher in the room. I explained that we could keep going with examples and we would never prove this for all numbers this way so put up the statement a% of b = b% of a. Using their skills from this week of lessons as well as their previous algebra knowledge and some scaffolded questioning, the students were able to gradually work out the proof. Some may argue that such skills of proof should not be appearing in Year 8 but if you were to see the faces of the students when they realised what they had achieved you would realise that we really need to think about how we can enable students to discover Maths for themselves more often. As proved with this very simple lesson, if students are scaffolded with the right questions and prompts/direction then they can access Maths that may seem quite tricky. The students left the lessons very happy with themselves.
Reflecting on this lesson, I think it was really powerful for showing how easily we can change up the teaching style and give the students to explore. When preparing the lesson, I needed to
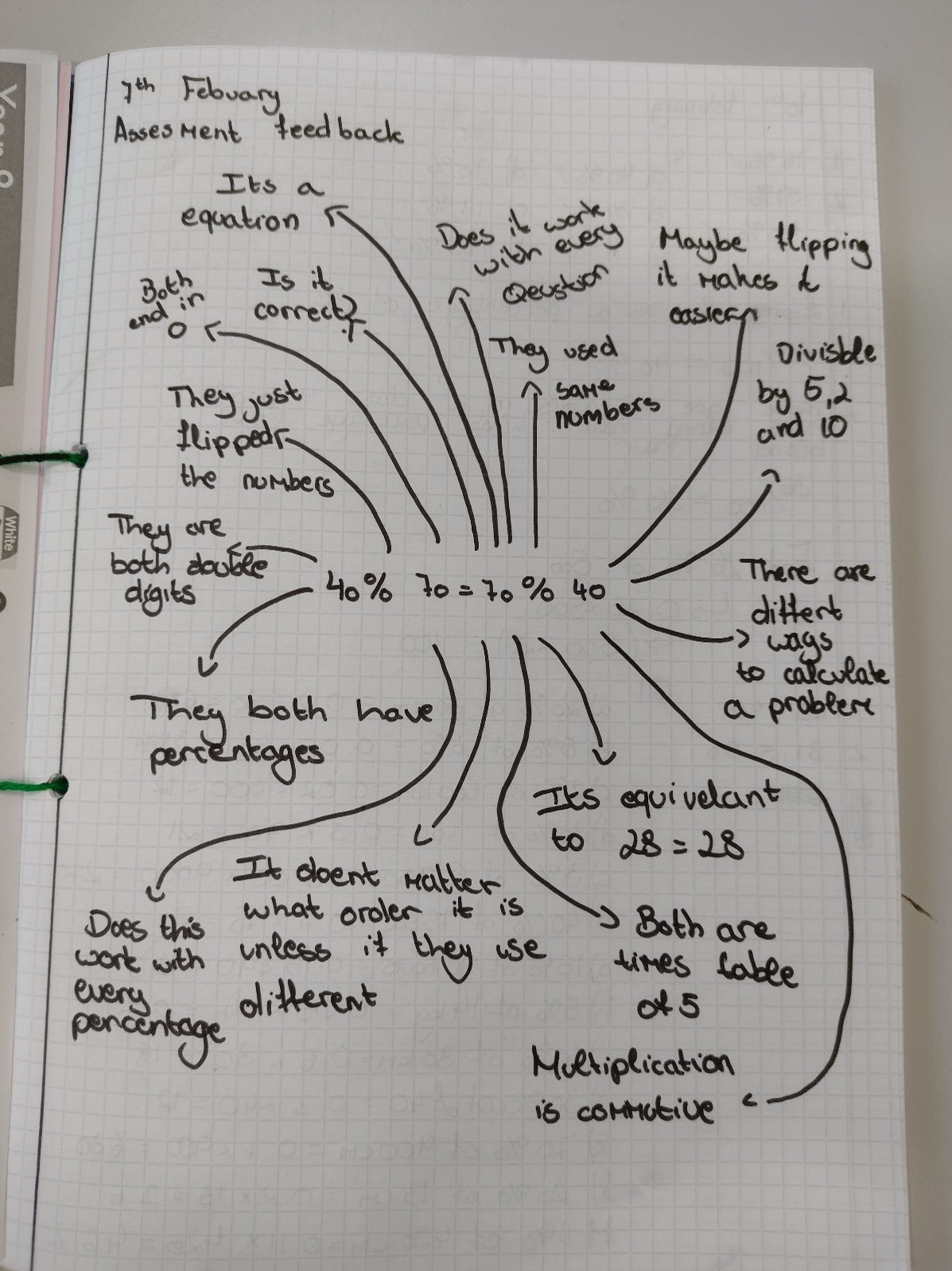consider carefully what questions I might ask to get the students thinking and what I would do if they really did struggle. However, other than this, it was a fairly simple lesson to prepare as the students did much of the thinking for themselves. I did have to spend a good amount of time at the beginning setting up my expectations for how the students needed to work and give them prompts of how to make observations and questions etc. If we engaged with this kind of learning more often, I would hopefully need to do less of this instruction each time. Areas of further development for this lesson could include changing the prompt to something like 20% of 40% of 70 = 70% of 40% of 20 or even by getting them to look at what happens when you increase or decrease.
This lesson was rich in student discussion, thinking and questioning which not only are skills needed for a good mathematician but also builds oracy and collaborative skills. I will be integrating more of this learning into my lessons where possible and hope to see it in the department too. We need to teach students skills and how to practice but we also need to teach them how to be a mathematician if we want to fully prepare them for their futures.
By Alfie Benson
------
Keep up-to-date with the latest Maths Scholarships news:
Find us on Twitter, Instagram, LinkedIn, YouTube, and Facebook.
Join our mailing list or get in touch Here.